A Simple Experiment
Proves π = 4
For those of you who want to go right to it without reading anything, here is the link to the youtube
video. It is only a few minutes long and contains no math. It is just two balls rolling through two
tubes. It was made by one of my students Steven Oostdijk, who is Dutch. He lives in the Netherlands.
In the first part of the video he is showing the viewers that he is not me. On Amazon.com and other
places, he has been accused of being me. This is because he has defended my theories there and in
other forums. As my readers know, I avoid forums, since I have a low tolerance for arguing with trolls.
I have better things to do. But many of my readers have more patience than I do, and some of them
like to defend me from these people—which of course is fine with me. Steven has been one of the
most outspoken and long lasting of my defenders. He is also very good at it, since he is an engineer
himself. Because of that, some have accused him of actually being me under another name. He isn't,
and this video proves that, among other more important things.
The video came about in this way: another student of mine, Jeff Cosman—who has been to several of
my conferences—devised a similar experiment using his children's toys. But since it was on wooden
tracks and looked a bit naïve at a first glance, I didn't want to post a link to it. It would have been too
easy to attack. So at my most recent conference this August, I suggested to my guys that they should
recreate the experiment with more precise instruments. One of them had told me he had access to a
machine shop and experiment lab, where things like this could be done at low or no cost. So he and a
couple of the other guys got started on the project after conference. A couple of days later Steven
emailed me and asked me how the conference went. I told him what I just told you, among other
things, and he asked me if he could take a stab at it as well, also having access to materials in his own
home. He said he thought he could get it done without leaving the garage. Which he pretty much did.
He had to leave the garage to get better light, but other than that it was all done at home. As for the
rest, he explains it in the video.
I have written a series of papers explaining why pi=4 whenever you have motion, but here I am going
to boil it down to the basics, for those who don't know much math or don't want to get into it. It can
get rather involved, and most people don't have the chops for it. Honestly, even professional
mathematians and physicists are having trouble following it, although it isn't that hard. It is hard only
in that it goes against everything we have been taught, and the old dogs of physics and math don't want
to learn any new tricks. So here I am going to assume you know absolutely nothing. I don't usually do
that, so forgive me if I tell you things you already know.
People just coming here from my art site won't understand why anyone would question pi. It seems
not only very old and established, but very basic. Most people will laugh and say something like, “I
didn't know there was any problem to solve there”. But there are problems and have been for a long
time, and insiders know that. Both in rocket science and quantum mechanics, big problems have
cropped up in the vicinity of pi, although no one before me thought to question pi itself. In the space
program, the engineers began seeing real-life failures of the equations from the beginning. In the late
1950s, the American program headed by Werner von Braun began admitting major equation failures.
Rockets simply weren't where they were supposed to be, but only when curved trajectories were
involved. The first rockets to orbit the earth were late by huge amounts, indicating the equations were
wrong by something over 20%. The Russians found the same problem. In press releases, they
indicated—and still indicate—the problem was with the propellants, but behind the scenes they pursued
other possibilities. Just as they assign equation failures now to dark matter, in the 1960's they asked
themselves if this rocket problem was caused by unknown ether's or forces of nature. As far as I know,
they still haven't solved it. It never occurred to them that pi might be the problem. As it turns out, the
failures in the rocket equations are exactly the same size as the gap between pi and 4.
A similar problem arose in quantum mechanics. Since quantum particles often move in orbits or
curved trajectories, the same sort of equation failures occurred there. The mainstream admits it has to
ditch classical geometry and resort to what is called the Manhattan metric to solve some quantum
problems. This is curious since in the Manhattan metric, pi=4.
Some have taken exception to my way of stating that. They say that pi is 3.14... and can't also be 4.
They say I should come up with another Greek letter, at the least. But pi isn't defined as 3.14. Pi is
defined as the ratio of the circumference and the diameter. I have proved that when motion is involved,
that ratio is 4. Therefore, it is correct to say that pi=4.
Others have said that even if I am right, it is just a quibble, since in most cases pi will still be 3.14. But
that simply isn't true. In physics—and therefore in the real-world—almost all uses of pi include
motion. When pi is used in physical equations, 99% of the time those equations include a velocity of
some sort. Which is why I provocatively titled my original paper “The Extinction of Pi.” In a few
years, the number 3.14... will be a virtual relic. It will also be a joke, since it will be a reminder of
how wrong mainstream physics can be.
But most will probably still not understand why it is true, even after watching a video that shows it.
Steven glosses it in the video, but most viewers won't find that helpful, I know. It doesn't seem right
that just turning a tube into a circle would make it longer. It looks at first like when you lay the tube
out straight, it is pi diameters long, but when you curve it into a circle, it magically becomes 21%
longer. Well, it doesn't really become longer, and we know that since we can straighten it back out and
it is still pi diameters long. But something about curving it changes it. It doesn't change the length, it
changes the distance that has to be traveled. The distance traveled in the curve can't be measured by
just measuring the straight length. When measuring the distance traveled along a straight line, you can
just use the length. The length tells you the distance traveled. But with a curve, that is no longer true.
Again, why?
I am going to try to explain it in the simplest possible way. To move in a curve, you have to combine
two motions. You have to move forward and sideways at the same time, right? So let's start with a
right triangle.
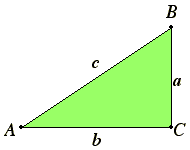
Let us say points A and B are on a circle, and you wish to travel from A to B. It seems like the simplest
thing to do would be to take the path c, since it is the most direct. You just cut straight across on the
hypotenuse. In fact, that is what the ancient Greeks assumed, and their original assumption has skewed
this problem ever since. It is still the assumption today. Mainstream physicists and mathematicians
still assume the circle is composed of a lot of little c-paths. They make the c-paths very tiny and then
sum them, giving them the circumference of the circle. But what I have shown is that they have
cheated. You can't take the path c, because it doesn't correctly represent the forward motion and the
sideways motion we just talked about. Obviously, the path a represents the forward motion and the
path b represents the sideways motion. Therefore, no matter how tiny you make that triangle, you
have to keep the a and b paths.
You will say, “C'mon, that can't be right! I can draw that triangle on the ground, and I can always walk
that c-path. There is nothing stopping me.” True, but if you are walking that c-path, you aren't walking
a curve, are you? You are walking a straight line. And if you combine a lot of those c-paths to try to
create a circle, you aren't really creating a circle. You are creating a polygon. Even if you make your
circle out of thousands of those c-paths, in each little triangle you are still cutting the corner. If you cut
the corner, you aren't representing forward motion and sideways motion at the same time in your fake
circle. So it isn't really a circle. You are not creating real circular motion.
You will say, “Even so, if I make those c-paths tiny enough, I will still get the right number for the
circumference of the circle. Everyone knows that.” In this case, what everyone “knows” is wrong. In
fact, if you cut all the corners in each little triangle, you end up getting a number for the circumference
that is way too small. It is 21% too small, which is a lot. It isn't a marginal error, it is huge miss.
You may still not understand, and in my other papers I explain it at much greater lengths, doing more
math. But if you haven't followed me here, you probably won't follow me there. However, if you ask
why the ball in the circular tube is taking so long to get around, the simplest answer is because it isn't
cutting the corners. It isn't taking the c-paths. It is taking the a and b paths.
[See addendum below for link to an animation that shows how the curved path is created with
perpendicular straight paths.]
If you have any friends who are mathematicians, they will tell you you have to know calculus to
understand this, but that is just a dodge. I just told you why it is true, without calculus. However, I will
tell you what they will say. They will say that when you integrate the a and b-paths, you get the c-path.
Integration is a calculus move. It is true that integration is involved here, but if you integrate
correctly, you don't get the c-path. The calculus they currently apply to this problem is right, but it is
wrongly applied. I may be able to make you understand why it is wrongly applied, even without
teaching you calculus.
The diagram of the triangle above is a simplification of the problem. It is a simplification because it
doesn't include time. It is geometric only. So although it is correct as far as it goes, it doesn't really tell
you the whole story. It helps you understand that the ball can't take the c-path, but it doesn't really tell
you exactly how the ball combines the two motions into the curve.
What you have just discovered is that the ball doesn't combine the a and b-paths. In other words, it
doesn't integrate them, in some magical calculus way. No matter how small you go or how many
little triangles you have on your circle, the a and b-paths remain distinct and at right angles to one
another. They never combine into a c-path. So why do we need calculus at all, you will ask?
Because, to solve this with math, we have to integrate both a and b with time t. In other words, we
don't integrate a with b, we integrate a with time t and b with the same time t. If you don't like the
word integrate—because it is a calculus term—I can say it this way: we have to track how a changes
with time and the way b changes with time. That's how we include time in the problem.
Currently, when physicists or mathematicians try to solve this problem with calculus, they basically leave
time out of it and track a against b. They integrate motion a with motion b to get motion c, which is
the c-path. But although the calculus they use to solve the problem is correct in itself, they are
applying it wrongly. Since all physics is applied math, you have to apply the math correctly. If you
apply the right math incorrectly, you will get the wrong answer.
This is why in my other papers I have offered the cycloid math as the solution here. A cycloid is a
rolling circle. The reason the cycloid math helps is that it explicitly includes the time variable. It
integrates three variables, a, b, and t. Beyond that, the cycloid math applies the variables to the
problem in the right way, so all we have to do it take the cycloid math and apply it to the distance
around the circle. It solves this problem perfectly, giving us the right answer: the circumference of the
circle is 8r.
But why would the cycloid math work here? Because if you are moving around a circle, it is like you
are moving around a circle that is rolling in place. In other words, it is like taking a rolling wheel, but
not letting it move forward. It is just spinning in place. You then position yourself at some point on
the rim of the wheel. As it moves around, so do you. You are then in circular motion. That is what
the current cycloid math actually represents.
#####################
I predict the main response to the video will be that the ball in the curve is feeling more friction.
However, it is clear at a glance this is not the case. To start with, the ball in the curve would have to be
feeling over 20% more friction than the straight ball. Again, the difference between 3.14 and 4 is not
marginal. It is huge. There is no way to account for a difference that large with a difference in friction.
Plus, if friction were the cause, the ball in the curve should be slowing down as it progresses around the
curve. Friction is of course cumulative, so we would expect a ball feeling an excess 21% of friction to
be going slower in the fourth quadrant of the circle than in the first. But we see with our own eyes that
isn't true. Steven marks all four quarter points in the circle, and the ball hits them all perfectly in sync
with the straight ball. If the ball in the curve were feeling more friction, we would expect it to hit the
¾ mark and final mark noticeably late compared to the ¼ mark. It doesn't. This indicates very strongly
that neither friction nor any other cumulative effect in the curve is causing the difference. The ball in
the curve is NOT slowing relative to the straight ball. This should look as curious to you as pi being 4.
Given current theory, it is just as mysterious.
Also consider this. If you are arguing there is more friction in the circle because the tube is curved, ask
yourself this: What are the odds that the extra friction in the circle would be exactly the amount to fill
the difference between pi and 4? Steven finds that when the ball is at the end of the circle, the straight
ball is exactly at 4. The circle ball also hits the other quarter points like clockwork. Do you really
think the curved tube is going to just miraculously provide the precise amount of friction to cause a
match at 4, and seem to prove my assertion? That would be even more unlikely than the experiment
itself. Steven would have to be some sort of magician or experimental genius to choose a plastic tube
from the hardware store that had just the right properties, so that when curved it had exactly 21% more
friction than when not curved, filling the gap between pi and 4. And, since he provides two
experiments with two different kinds of tubing, he would have to do that twice, just lucking upon two
different hardware store tubes that both magically provided this 21% differential in friction.
####################
That said, most people will still not understand how I thought to question such a thing. I am not a
famous quantum physicist or NASA scientist. Plus, I admit I didn't even know about those rocket and
quantum problems when I solved this. I only found them as confirmation after the fact. I didn't know
about Werner von Braun's equation problems until after writing my pi papers. I didn't know about the
Manhattan metric until four years after I wrote the original paper on pi. I didn't even link this to the
cycloid math—where pi is also 4—until several years later. So how did I manage to solve a problem I
didn't even know existed?
Well, I came at it kind of sideways, since I was solving related problems. It wasn't known the problems were related until I showed it, but they are. I was working on Newton's orbital equations, which I saw as having some disclarities. To say it another way, they didn't make sense to me. I thought his proofs contained some big holes, and the more recent updates of these proofs by famous guys like Richard Feynman seemed to me no better. In fact, I showed they were worse.
Since an orbit is just motion in a circle, I think you can see the link. So I started over from the beginning, rerunning Newton's equations with a few corrections. These corrections solved many problems, but not all of them. It wasn't until a couple of years later that I thought to look at pi itself. My corrections to the orbital equations suggested that pi simply couldn't be right. I found that the old orbital equations—including Newton's—were naively based on Euclid's geometry, which didn't include time. The geometry you learn in school doesn't include any velocities. It only includes lengths. If you calculate pi in geometry—with no time and no velocities—you do indeed get the number 3.14... But in physics that math isn't useful. In physics you almost always have a motion you are tracking, so time is involved. You have to replace every length with a velocity. And if you do that, you can't use Euclid's geometry. It doesn't have enough variables. You are always a variable short.
This means that the old orbital math was always a variable short. It was incomplete. It didn't include time. Because it didn't include time, it couldn't represent the real world. It could only work in a book problem, where everything was happening at some imaginary instant. This ended up making all the math explode. In quantum mechanics there is a thing called renormalization. It is what they have to do to equations that have exploded. Basically, when you try to solve real-life problems with equations that don't properly include the time variable, your equations start spitting out zeroes and infinities. In quantum mechanics, this happens to all their equations, and they admit that. They admit it, but don't understand why.
In other words, they are trying to solve kinematic problems with geometry. It would be like trying to paint with a pencil. You can't paint with a pencil, because you don't have any color. Likewise, you can't solve physics problems with geometry, because you don't have time. They try to stir time back into the equations at the end, but it has never worked.
They offer million dollar prizes (see Claymath) to anyone who can solve these problems. . . except me. What they want is a big impressive looking solution: you know, one of those solutions that fills the blackboard with funny squiggles. They don't want to be told that they have the wrong number for pi, or that Newton made a simple mistake, or anything like that. That is just embarrassing. And they especially don't want to hear it from me. They want one of their gold-plated colleagues—one of the guys in a chair at Oxford or something—to solve it.
You will say, “Well, why don't they just install you in some chair like that? Then they can save face”. They had their chances to do that, but they chose not to. They could have brought me into the fold and been nice, but they chose to try to bury me. About 17 years ago, I began sending my papers to mainstream sources, trying to play by the rules. But they decided to be nasty, not just refusing the papers, but implying I was some sort of idiot for disagreeing with them. And when I began self publishing on the web a few years later, they got really nasty. They hired a bunch of trolls to slander me all over the web, stopping at nothing. Rather than respond rationally or scientifically to my ideas, they instead attacked me personally, often with outright lies. They hired people to review my books who hadn't read them. They attacked my hair. They attacked my paintings. They attacked my poetry. They attacked me for having taken ballet in college.
They are still doing it, and they often lead with my pi papers. Often, when they need a knee jerk response to me, they dismiss me as “the guy who thinks pi=4”. But rather than back down, I have embraced that, and you are now seeing why I always embraced it. I WANTED TO BE KNOWN AS THAT GUY. Because now, as it is becoming clear I was right, it is going to be very hard for them to steal the idea from me. I still suspect they will try to steal it, but a lot of people are going to go, “Hey, wait a minute, isn't that what that 'crank' Miles Mathis was telling us a few years ago? And now you guys are trying to steal it?”
That is what it means when you are told that all publicity is good publicity. All the controversy just means people know who I am. It is harder to steal from a known entity. Since no one else was “rash” enough to claim pi=4, I am the only pi=4 guy. So when it is generally admitted that pi=4, I am the only guy who can be linked to that, you see? Except that I don't just laugh last, I have been laughing all along.
Now, after you watch the video several times, ask yourself this: how is it that this is the first time you are seeing this? This is a very simple experiment, right? Pi has been around for what, 5000 years, and no one ever thought to check it in this way? They now spend billions of dollars searching for dark matter and gravitons and so on, but no one ever thought to do a simple experiment to see if pi was right? This just confirms what I have said many times before: mainstream physics is now about milking money from the treasury, and real physics just isn't expensive enough. Basic experiments aren't run because it doesn't pay to run them. You can run this experiment yourself for under $100, so big physics departments and institutions aren't interested in it. It won't pay anyone's salary. It also doesn't pay because the result destroys decades and centuries of mainstream physics. Put simply, it is bad for business, or is thought to be. It blows a big hole in the physics story you are told, in which mainstream physicists are geniuses saving the world. No, seriously, they actually say that about themselves in mainstream publications. This is what leads you to support all their billion-dollar projects. But once you see they don't even understand circular motion or calculus, all that evaporates. You realize they are just as incompetent as the guy working on your car or installing your new hot tub —actually a lot more so—and far more arrogant.
Real physics can be good business but those at the top of the field now don't see that. They have created a paradigm that works for them and they naturally wish to stick with it. That paradigm consists of selling huge fake projects and doing no real physics. Exchanging their fake physics for real physics will require a complete overhaul of the field and they have no desire to see that happen. This is also understandable, since it entails them being tossed out on their asses. These problems I have solved aren't the end of physics, or even mainstream physics, but they are the end of some people's careers, and they recognize that. All the top dogs are going to go down in flames, and good riddance. The problem is, they are hoping to ride it out. They hope that by stalling as long as possible, they can retire or die before the revolution hits, saving them from the retribution they have so justly earned. Supposing their ghosts aren't forced to watch the revolution anyway, that may work for them to a small degree. But mostly it will fail, because my students and I will make sure their deeds are known regardless. After the revolution, there will be no one to whitewash them.
That is another thing these people don't understand about life: just as it is impossible to cut corners in the circle, it is impossible to dodge responsibility for your actions. Not even death will save them. Some call it judgment, some call it karma, but one thing is certain: the past has a way of making itself known to the present, since it is embedded in the present. The truth will out. Sometimes it takes centuries, but the truth is eventually discovered. Once it is, the future utterly overwhelms the past.
To take an example from the past century, Niels Bohr has been famous for about 90 years. But after the revolution, he will be infamous for millennia. He chose his side, and so must you. I did.
The top dogs can still switch sides. It is never too late. They can save their own eternal reputations to a large degree by apologizing and coming clean today. It can happen, and has happened a few times in history. You sometimes witness an 11th hour move from the dark side to the light, and the saving of a soul. Like anything else, karma can be cleansed.
For further proof, I recommend you study this animation sent to me by a reader John McVay. He developed this from a similar animation he saw in an old 1986 Mechanical Universe segment on PBS. You can see this segment—originally produced by Caltech at Annenberg Learner Go to minute 11:15 of episode 9 to see the fuller animation. In both the Caltech and McVay animations, we see how the circle is produced straight from orthogonal vectors. In the Caltech animation, it is clear that no diagonal is ever produced: the motion is a simple addition of x and y. Neither x nor y ever move on an hypotenuse (c-path), therefore the combined motion cannot do so, either. This animation is just a speeded-up step method, and therefore pi would equal four here.
[I previously had a youtube link posted of this Mechanical Universe segment. Within a few weeks of my link, the youtube videos were removed by the poster. Here we see more obstruction of science by the mainstream. Rather than allow an alternate interpretation of data, they prefer to remove the data. Or, they post the data only as long as it only sells their own interpretation. If anyone discovers a better interpretation—one that undercuts the original propaganda—they have to remove the data. That is perfect anti-science. The scientific method would be either to counter the new interpretation, showing how it is wrong; or to allow both interpretations to stand, letting the readers decide which was stronger. But that isn't the method of the mainstream, and hasn't been for decades. They hide all negative data, and when any of their old “positive” data or demonstrations are questioned, they simply remove them from sight as well. That is a pseudo-science grounded in authority, censorship, obstruction, and misdirection. These people prove my point with everything they do. The subtitle of the series was originally “Mechanical Universe: Expand your Mind”. I guess they will have to change that to “Mechanical Universe: Deleted to Suppress Your Mind”.
You can still take the link to McVay's video above.
Breaking News: a reader found a copy of the Mechanical Universe video on Daily Motion.com. Also it just went back up at youtube, by a different poster. Watch it while it is up! And please, anyone who has the technology, download it. I used to be able to do it on my old computer, but not on this one. It is sure to be deleted again.
October 9, 2016: the youtube repost lasted 2 days after I posted my link. It has been removed due to a copyright claim by “Intelecom Intelligent Communications”. Someone really doesn't want you to see that video. You may want to ask yourself why mainstream science is trying so hard to suppress one of its own educational videos. Before I came along, these videos were up on youtube for years.
November 8, 2016: I have had one of my online buddies create a gif for me that matches part of the video they are suppressing. I have never imported a gif into a paper before, so hopefully this will work, including the motion. See below.
If that doesn't move for you, you can go to his video at Vimeo.
While I am here on this update, I want to point out that the viewer numbers of Steven's pi=4 Youtube video are being suppressed. After climbing quickly for a few days, they suddenly went stagnant. You will tell me everyone in the world who might be interested in such a topic viewed the video in the first week, after which interest completely died out. But that isn't true and I know it. I know it because I purposely visited the page many times in one day, taking note of the numbers before and after. There was no movement in the numbers. This reminded me of the last time I voted. The voting machines have visible counters on them, and I knew to watch the counter. I noted the number before I voted, then voted, then noted the number after: it didn't change. I therefore knew my vote had not been counted. When I told this to the local authority, she expressed no interest. She didn't even look surprised. She offered me no possible solution, not even a complaint form or an address to send a notification of vote fraud.
While Steven's numbers are being suppressed, surrounding videos on pi with no discernible content (except misdirection) are being heavily promoted, and their numbers inflated by what I assume are huge amounts. Videos by obvious trolls from sub-basement 7 at the Pentagon or somewhere have what we are told are millions of hits, although personally I don't believe it. To start with, they are too new to have that many hits. And since they address the pi=4 problem, discovered by me, there is no way my friend's video on the problem can have a few thousand hits, while responses to it can have millions. Why would someone click on a video that is a response to a problem, without first clicking on the problem itself? It is illogical.
http://milesmathis.com/pi7.pdf
Well, I came at it kind of sideways, since I was solving related problems. It wasn't known the problems were related until I showed it, but they are. I was working on Newton's orbital equations, which I saw as having some disclarities. To say it another way, they didn't make sense to me. I thought his proofs contained some big holes, and the more recent updates of these proofs by famous guys like Richard Feynman seemed to me no better. In fact, I showed they were worse.
Since an orbit is just motion in a circle, I think you can see the link. So I started over from the beginning, rerunning Newton's equations with a few corrections. These corrections solved many problems, but not all of them. It wasn't until a couple of years later that I thought to look at pi itself. My corrections to the orbital equations suggested that pi simply couldn't be right. I found that the old orbital equations—including Newton's—were naively based on Euclid's geometry, which didn't include time. The geometry you learn in school doesn't include any velocities. It only includes lengths. If you calculate pi in geometry—with no time and no velocities—you do indeed get the number 3.14... But in physics that math isn't useful. In physics you almost always have a motion you are tracking, so time is involved. You have to replace every length with a velocity. And if you do that, you can't use Euclid's geometry. It doesn't have enough variables. You are always a variable short.
This means that the old orbital math was always a variable short. It was incomplete. It didn't include time. Because it didn't include time, it couldn't represent the real world. It could only work in a book problem, where everything was happening at some imaginary instant. This ended up making all the math explode. In quantum mechanics there is a thing called renormalization. It is what they have to do to equations that have exploded. Basically, when you try to solve real-life problems with equations that don't properly include the time variable, your equations start spitting out zeroes and infinities. In quantum mechanics, this happens to all their equations, and they admit that. They admit it, but don't understand why.
In other words, they are trying to solve kinematic problems with geometry. It would be like trying to paint with a pencil. You can't paint with a pencil, because you don't have any color. Likewise, you can't solve physics problems with geometry, because you don't have time. They try to stir time back into the equations at the end, but it has never worked.
They offer million dollar prizes (see Claymath) to anyone who can solve these problems. . . except me. What they want is a big impressive looking solution: you know, one of those solutions that fills the blackboard with funny squiggles. They don't want to be told that they have the wrong number for pi, or that Newton made a simple mistake, or anything like that. That is just embarrassing. And they especially don't want to hear it from me. They want one of their gold-plated colleagues—one of the guys in a chair at Oxford or something—to solve it.
You will say, “Well, why don't they just install you in some chair like that? Then they can save face”. They had their chances to do that, but they chose not to. They could have brought me into the fold and been nice, but they chose to try to bury me. About 17 years ago, I began sending my papers to mainstream sources, trying to play by the rules. But they decided to be nasty, not just refusing the papers, but implying I was some sort of idiot for disagreeing with them. And when I began self publishing on the web a few years later, they got really nasty. They hired a bunch of trolls to slander me all over the web, stopping at nothing. Rather than respond rationally or scientifically to my ideas, they instead attacked me personally, often with outright lies. They hired people to review my books who hadn't read them. They attacked my hair. They attacked my paintings. They attacked my poetry. They attacked me for having taken ballet in college.
They are still doing it, and they often lead with my pi papers. Often, when they need a knee jerk response to me, they dismiss me as “the guy who thinks pi=4”. But rather than back down, I have embraced that, and you are now seeing why I always embraced it. I WANTED TO BE KNOWN AS THAT GUY. Because now, as it is becoming clear I was right, it is going to be very hard for them to steal the idea from me. I still suspect they will try to steal it, but a lot of people are going to go, “Hey, wait a minute, isn't that what that 'crank' Miles Mathis was telling us a few years ago? And now you guys are trying to steal it?”
That is what it means when you are told that all publicity is good publicity. All the controversy just means people know who I am. It is harder to steal from a known entity. Since no one else was “rash” enough to claim pi=4, I am the only pi=4 guy. So when it is generally admitted that pi=4, I am the only guy who can be linked to that, you see? Except that I don't just laugh last, I have been laughing all along.
Now, after you watch the video several times, ask yourself this: how is it that this is the first time you are seeing this? This is a very simple experiment, right? Pi has been around for what, 5000 years, and no one ever thought to check it in this way? They now spend billions of dollars searching for dark matter and gravitons and so on, but no one ever thought to do a simple experiment to see if pi was right? This just confirms what I have said many times before: mainstream physics is now about milking money from the treasury, and real physics just isn't expensive enough. Basic experiments aren't run because it doesn't pay to run them. You can run this experiment yourself for under $100, so big physics departments and institutions aren't interested in it. It won't pay anyone's salary. It also doesn't pay because the result destroys decades and centuries of mainstream physics. Put simply, it is bad for business, or is thought to be. It blows a big hole in the physics story you are told, in which mainstream physicists are geniuses saving the world. No, seriously, they actually say that about themselves in mainstream publications. This is what leads you to support all their billion-dollar projects. But once you see they don't even understand circular motion or calculus, all that evaporates. You realize they are just as incompetent as the guy working on your car or installing your new hot tub —actually a lot more so—and far more arrogant.
Real physics can be good business but those at the top of the field now don't see that. They have created a paradigm that works for them and they naturally wish to stick with it. That paradigm consists of selling huge fake projects and doing no real physics. Exchanging their fake physics for real physics will require a complete overhaul of the field and they have no desire to see that happen. This is also understandable, since it entails them being tossed out on their asses. These problems I have solved aren't the end of physics, or even mainstream physics, but they are the end of some people's careers, and they recognize that. All the top dogs are going to go down in flames, and good riddance. The problem is, they are hoping to ride it out. They hope that by stalling as long as possible, they can retire or die before the revolution hits, saving them from the retribution they have so justly earned. Supposing their ghosts aren't forced to watch the revolution anyway, that may work for them to a small degree. But mostly it will fail, because my students and I will make sure their deeds are known regardless. After the revolution, there will be no one to whitewash them.
That is another thing these people don't understand about life: just as it is impossible to cut corners in the circle, it is impossible to dodge responsibility for your actions. Not even death will save them. Some call it judgment, some call it karma, but one thing is certain: the past has a way of making itself known to the present, since it is embedded in the present. The truth will out. Sometimes it takes centuries, but the truth is eventually discovered. Once it is, the future utterly overwhelms the past.
To take an example from the past century, Niels Bohr has been famous for about 90 years. But after the revolution, he will be infamous for millennia. He chose his side, and so must you. I did.
The top dogs can still switch sides. It is never too late. They can save their own eternal reputations to a large degree by apologizing and coming clean today. It can happen, and has happened a few times in history. You sometimes witness an 11th hour move from the dark side to the light, and the saving of a soul. Like anything else, karma can be cleansed.
Addendum, October 4, 2016:
I wanted to post a link to a CalTech video which supports my triangle
interpretation above, but found it has been deleted all over the web. In my paper on the Manhattan Metric from 2012, I said this: For further proof, I recommend you study this animation sent to me by a reader John McVay. He developed this from a similar animation he saw in an old 1986 Mechanical Universe segment on PBS. You can see this segment—originally produced by Caltech at Annenberg Learner Go to minute 11:15 of episode 9 to see the fuller animation. In both the Caltech and McVay animations, we see how the circle is produced straight from orthogonal vectors. In the Caltech animation, it is clear that no diagonal is ever produced: the motion is a simple addition of x and y. Neither x nor y ever move on an hypotenuse (c-path), therefore the combined motion cannot do so, either. This animation is just a speeded-up step method, and therefore pi would equal four here.
[I previously had a youtube link posted of this Mechanical Universe segment. Within a few weeks of my link, the youtube videos were removed by the poster. Here we see more obstruction of science by the mainstream. Rather than allow an alternate interpretation of data, they prefer to remove the data. Or, they post the data only as long as it only sells their own interpretation. If anyone discovers a better interpretation—one that undercuts the original propaganda—they have to remove the data. That is perfect anti-science. The scientific method would be either to counter the new interpretation, showing how it is wrong; or to allow both interpretations to stand, letting the readers decide which was stronger. But that isn't the method of the mainstream, and hasn't been for decades. They hide all negative data, and when any of their old “positive” data or demonstrations are questioned, they simply remove them from sight as well. That is a pseudo-science grounded in authority, censorship, obstruction, and misdirection. These people prove my point with everything they do. The subtitle of the series was originally “Mechanical Universe: Expand your Mind”. I guess they will have to change that to “Mechanical Universe: Deleted to Suppress Your Mind”.
Addendum October 2016:
They have now removed the video from Annenberg Learner as well.
They should change the name of the site to Annenberg Anti-Science. I checked youtube to see
if someone had reposted it there, but CalTech has actually deleted almost all its Mechanical
Universe videos. As you see here, you can still subscribe to this old series, but once you get in,
almost all the videos have been deleted. Man, have I got these people on the run!] You can still take the link to McVay's video above.
Breaking News: a reader found a copy of the Mechanical Universe video on Daily Motion.com. Also it just went back up at youtube, by a different poster. Watch it while it is up! And please, anyone who has the technology, download it. I used to be able to do it on my old computer, but not on this one. It is sure to be deleted again.
October 9, 2016: the youtube repost lasted 2 days after I posted my link. It has been removed due to a copyright claim by “Intelecom Intelligent Communications”. Someone really doesn't want you to see that video. You may want to ask yourself why mainstream science is trying so hard to suppress one of its own educational videos. Before I came along, these videos were up on youtube for years.
November 8, 2016: I have had one of my online buddies create a gif for me that matches part of the video they are suppressing. I have never imported a gif into a paper before, so hopefully this will work, including the motion. See below.
If that doesn't move for you, you can go to his video at Vimeo.
While I am here on this update, I want to point out that the viewer numbers of Steven's pi=4 Youtube video are being suppressed. After climbing quickly for a few days, they suddenly went stagnant. You will tell me everyone in the world who might be interested in such a topic viewed the video in the first week, after which interest completely died out. But that isn't true and I know it. I know it because I purposely visited the page many times in one day, taking note of the numbers before and after. There was no movement in the numbers. This reminded me of the last time I voted. The voting machines have visible counters on them, and I knew to watch the counter. I noted the number before I voted, then voted, then noted the number after: it didn't change. I therefore knew my vote had not been counted. When I told this to the local authority, she expressed no interest. She didn't even look surprised. She offered me no possible solution, not even a complaint form or an address to send a notification of vote fraud.
While Steven's numbers are being suppressed, surrounding videos on pi with no discernible content (except misdirection) are being heavily promoted, and their numbers inflated by what I assume are huge amounts. Videos by obvious trolls from sub-basement 7 at the Pentagon or somewhere have what we are told are millions of hits, although personally I don't believe it. To start with, they are too new to have that many hits. And since they address the pi=4 problem, discovered by me, there is no way my friend's video on the problem can have a few thousand hits, while responses to it can have millions. Why would someone click on a video that is a response to a problem, without first clicking on the problem itself? It is illogical.
http://milesmathis.com/pi7.pdf
None of the links in your post are working. I am getting a site cannot be reached notification on each link.
ReplyDeletehttps://www.youtube.com/watch?v=QhuvUSS3KAE
DeleteYeah I see that, not surprising,the powers that be, do not like being made fools of and are suppressing this big time, I am going to add a direct link to the paper at Miles site, maybe those will work, if not the GIF is on it, sorry about this Thom
Delete